Collatz conjecture experiments

this section contains some experiments on the collatz conjecture which has deep connections to TCS.[4][19] this is the nagging, taunting, ¾-century-unsolved problem for which Erdös semifamously said:

Mathematics is not yet ripe for such problems. —Erdös

also Terrence Tao immediately cites it when referring to “mathematical diseases”[9] and as “One of the most notorious problems in elementary mathematics that remains unsolved”.[7] he compares succeeding on such problems to “winning the lottery” and even somewhat dramatically admonishes/warns against working on such problems, in line with that old canard…

fools rush in where angels fear to tread

maybe appropriately, the following is a work-in-progress & admittedly sketchy.

⭐ ⭐ ⭐

the Collatz conjecture is a great problem to experiment/study on esp with CS based approaches (writing code, visualizing results); its possible/ ultimate/ eventual(?) solution is regarded as very hard—or maybe impossible—by experts. however there are many basic variants of exercises on it that have “correct solutions” that are accessible to undergraduates. it has remarkable/amazing aspects of/connections to many areas of active mathematical & CS research, in a few words, highly crosscutting, suggesting a tip of an iceberg:

• fractals
• chaotic behavior
• dynamical systems
• number theory
• (un)decidability
• busy beaver problem
• automata theory
• Finite state transducer
• random walks
• pseudorandom number generators
• emergent behavior
• open problem
• discrete mathematics
• differential equation
• recurrence/ difference equation
• coding theory
• experimental mathematics
• data mining
• cryptography
• scientific visualization
• graph theory
• ergodic theory
• probabilistic number theory
• strange attractor
• statistics / data analysis
• big data
• automated theorem proving
• complexity / complex systems
• tag system
• computational complexity theory
• phase transition
• cellular automata
• Turing machine
• mathematical induction, inductive reasoning, problem of induction
• machine learning
• statistical arbitrage
• control theory
• citizen science
• information theory
• statistical physics
• signal processing
• stochastic calculus

⭐ ⭐ ⭐

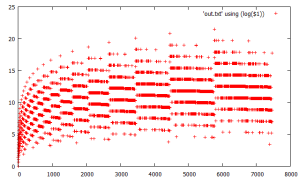
my major unique homegrown angle into this is a sort of datamining/near-hacking approach of writing simple programs to transform the function in key ways. this has led to many different angles and visualizations on the problem and have many assorted blogs on this approach now over the past half year (2013). heres a neat new one just generated, surprisingly simple yet evocative (the general goal of such exercises). it outputs integers in reverse order starting from 2 in a breadth-first expansion of the graph (logarithmic y axis). a fractal pattern of traversing higher integers is quite evident. (cant you just see the inductive proof leaping out at you?) 😀

l = [2]

seen = {}
30.times \
{
	l2 = []
	l.each \
	{
		|x|
		l1 = [x * 2]
		l1 << (x - 1) / 3 if (x % 3 == 1)
		l1.each \
		{
			|x2|
			next if (seen.member?(x2))
			seen[x2] = nil
			l2 << x2
		}
	}
	l = l2
	l2.each { |x| p(x) }
}

a remarkable correlation is that the following program which uses a real PRNG instead and a very slight alteration in logic to generate a very similar diagram, nearly visually indistinguishable, thereby emphasizing the connection of the algorithm to PRNGs.

l = [2]

srand

seen = {}
34.times \
{
	l2 = []
	l.each \
	{
		|x|
		l1 = [x * 2]
		l1 << x / 3 if (rand(3) == 0)
		l1.each \
		{
			|x2|
			next if (seen.member?(x2))
			seen[x2] = nil
			l2 << x2
		}
	}
	l = l2
	l2.each { |x| p(x) }
}

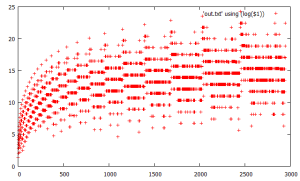
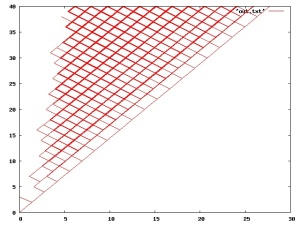
heres another simple program that produces interesting/remarkable/fractal-looking results. it simply enumerates in reverse order in a breadth-first fashion starting at 1 in this case for 42 levels of “breadth”, with the y coordinate the level associated with the x coordinate point.

l = [1]
seen = {}

42.times \
{
        |i|
        l2 = []
        l.each \
        {
                |x|
                l3 = []
                l3 << x * 2
                l3 << (x - 1) / 3 if (x % 3 == 1)
                l3.each \
                {
                        |x2|
                        next if (seen.member?(x2))
                        seen[x2] = i
                        l2 << x2
                }
        }
        l = l2
}

seen.keys.sort.each \
{
        |i|
        puts([i, seen[i]].join("\t"))
}

here is a slight modification of the prior algorithm that draws connections/lines between the levels and is reminiscent of the concept of tilings. (the first is exactly as discovered, a second version of the code is similar but conceptually simpler without the postprocessing logic/loop.)

l = [1]
seen = {}

40.times \
{
        |i|
        l2 = []
        l.each \
        {
                |x|
                l3 = []
                l3 << x * 2
                l3 << (x - 1) / 3 if (x > 1 && x % 3 == 1)
                l3.each \
                {
                        |x2|
                        next if (seen.member?(x2))
                        seen[x2] = [x, i]
                        l2 << x2
                }
        }
        l = l2
}

seen.each \
{
        |x2, xi|
        x, i = xi

        puts([Math.log(x), i].join("\t"))
        puts([Math.log(x2), i + 1].join("\t"))
        puts
}

l = [1]
seen = {}

40.times \
{
	|i|
	l2 = []
	l.each \
	{
		|x|
		l3 = []
		l3 << x * 2
                l3 << (x - 1) / 3 if (x > 1 && x % 3 == 1)
		l3.each \
		{
			|x2|
			puts([Math.log(x), i].join("\t"))
			puts([Math.log(x2), i+1].join("\t"));
			puts

			next if (seen.member?(x2)) 

			seen[x2] = nil

			l2 << x2
		}
	}
	l = l2
}

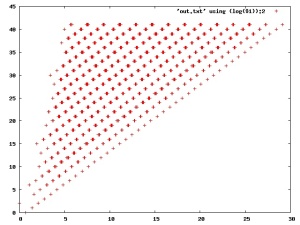
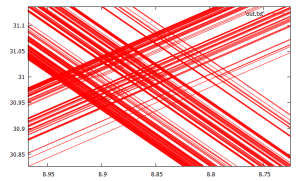
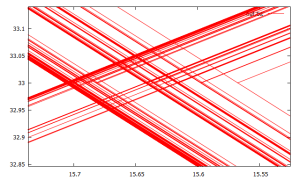
the following figures reveal the remarkable dichotomy of order and chaos in this visualization strategy. the above plots can barely look more ordered. however zooming in on the crosses/junctions/intersections of the lines reveals a chaotic pattern reminiscent of the rings of saturn (note these plots were generated by slightly different code):

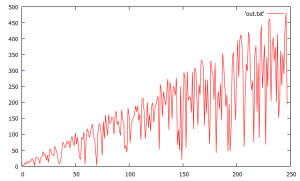
the earlier diagram showed how similar the collatz problem is to a PRNG (pseudo random number generator). this following concept expands on this from another angle. one might wonder if any program with random-looking output similar to the collatz trajectories could visit all integers. this is answered in the affirmative with this basic idea. start with an array of integers . then move an expanding window “leftward to rightward”. shuffle the elements of the array within the window each time. then output integers that are to the left of the sliding array (and are therefore not scrambled further). what does that look like?

the result is not so dissimilar to some Collatz outputs that go in reverse order starting from 1 and output visited integers. but this also again shows how much the proof of the Collatz conjecture would seem to be similar to breaking a PRNG (which deterministically controls the scrambling). in the following and the highest index of the array output is about ~250. (the algorithm generalizes to arbitrarily large .) in other words the diagram probably contains exactly once every integer — exercise: why not surely?

c = 500
l = (1..c).to_a

n = 0
m = 5

while (n + m <= l.size)

	l2 = l[n, m]
	l[n, m] = []

	l2.shuffle!

	l[n, 0] = l2

	p(l[n])

	n += 1
	m += 1

end

⭐ ⭐ ⭐

the other approach Ive followed for many years is to construct a FSM transducer for iterations as described on the wikipedia page, “as an abstract machine that computes in base 2” [3] although the origination of the technique is not so clear.[5] the FSM transducer computes iterates. built the transducer in the mid 1990s along with various auxiliary tools mainly for FSM logic. in the early ~2000s used the AT&T FSM library in many ways with this unique formulation.[6]

this approach has some strong connections to Shallit & Wilson [1] and is also similar to [2].

via this angle have found various interesting properties that probably have not been explored in the literature [which is large & forbidding, see eg the excellent survey/bibliography by Lagarias cited in [5]]. however, a proof is still elusive.

the general idea was/is to do a kind of experimental/empirical “datamining” on the algorithmic innards of the problem. this has led to many different views/angles/perspectives/analyses of the problem but (surprise!) not to a breakthrough so far.

fsm3nb.txt

this is the Collatz FSM iterate transducer. the and (state-from, state-to) are given in the 1^st and 2^nd column. the 3^rd column is the input digit. the 4^th column is the output digit. a 0 in the input or output column indicates ie the empty string. the transducer computes iterates of the Collatz problem in binary, specified in lsb to msb order (least significant to most significant bit). binary digits are specified as pairs. the pair 11 indicates binary bit and 12 indicates bit . the input number is terminated with the digit 2 in the first position. the final/end state is 30 with no new state, input, or output.

0       10      1       0
10      20      2       0
10      0       1       0
20      50      1       0
40      50      1       0
40      30      2       122
50      60      1       0
50      80      2       12
60      70      1       0
70      140     1       12
70      40      2       0
80      90      1       0
80      30      2       11122
90      100     1       11
90      80      2       12
100     110     1       0
110     140     1       12
110     80     2       11
120     130     1       0
120     30      2       122
130     140     1       12
130     80     2       11
140     150     1       0
150     140     1       11
150     120     2       12
30

similar except that the output field allows a string instead of single character. more compact & easier to deal with in some ways but AT&T FSM library does not support this format.

#!/usr/bin/ruby1.8

def fwd(x, b, fsm)

        s, i, o = x

        return nil if (fsm[s][b].nil?)

        s2, i2, o2 = fsm[s][b]

        while (!fsm[s2][0].nil?)
                s2, i3, o3 = fsm[s2][0]
                o2 += o3

        end

        y = [s2, i + i2, o + o2]
#       p([x, b.to_s + '=>', y])

        return y

end

def fsm(fn)

        fsm = {}
        File.open(fn).each \
        {
                |ln|

                l = ln.split
                l[0] = l[0].to_i
                fsm[l[0]] = [] if (fsm[l[0]].nil?)
                next if (l.size == 1)
                l[1] = l[1].to_i
                l[3] = '' if (l[3] == '0')
                fsm[l[0]][l[2].to_i] = l[1..3]
        }

        return fsm
end

def bin(l2)
        l2 = l2.dup

        raise if (l2.size % 2 == 0)
        raise if (l2.pop != 2)

        l3 = []
        while (!l2.empty?)
                raise if (l2.shift != 1)
                l3 << (l2.shift - 1)
        end

        l4 = l3.dup

        n = 0
        b = 1
        while (!l3.empty?)
                n |= (l3.shift * b)
                b <<= 1
        end

        return n

end

def f(n)

	n = n * 3 + 1
	n /= 2 while (n.even?)
	return n
end

def str2bin(s)

	return s.split('').map { |x| x.to_i }
end

def fwd2(l, fsm)

	x = [0, '', '']
	l.each \
	{
		|b|
		x = fwd(x, b, fsm)
		return if (x.nil?)
	}
	return str2bin(x[2])
end

def seq(fsm, fsm2)

        l = [1, 2, 1, 2, 1, 1, 1, 2, 1, 2, 2]
	n = 27
	c = 1
        loop \
        {
		l2 = fwd2(l, fsm)
		break if (l2.nil?)

		l3 = fwd2(l, fsm2)

		n = f(n)
                p([c, bin(l), n, bin(l2), bin(l3)])
                l = l2
		c += 1
        }

end

fsm = fsm('fsm3nb.txt')

fsm2 = fsm('fsm3nc.txt')

#p(fsm)
#p(fsm.keys)

seq(fsm, fsm2)

[1, 27, 41, 41, 41]
[2, 41, 31, 31, 31]
[3, 31, 47, 47, 47]
[4, 47, 71, 71, 71]
[5, 71, 107, 107, 107]
[6, 107, 161, 161, 161]
[7, 161, 121, 121, 121]
[8, 121, 91, 91, 91]
[9, 91, 137, 137, 137]
[10, 137, 103, 103, 103]
[11, 103, 155, 155, 155]
[12, 155, 233, 233, 233]
[13, 233, 175, 175, 175]
[14, 175, 263, 263, 263]
[15, 263, 395, 395, 395]
[16, 395, 593, 593, 593]
[17, 593, 445, 445, 445]
[18, 445, 167, 167, 167]
[19, 167, 251, 251, 251]
[20, 251, 377, 377, 377]
[21, 377, 283, 283, 283]
[22, 283, 425, 425, 425]
[23, 425, 319, 319, 319]
[24, 319, 479, 479, 479]
[25, 479, 719, 719, 719]
[26, 719, 1079, 1079, 1079]
[27, 1079, 1619, 1619, 1619]
[28, 1619, 2429, 2429, 2429]
[29, 2429, 911, 911, 911]
[30, 911, 1367, 1367, 1367]
[31, 1367, 2051, 2051, 2051]
[32, 2051, 3077, 3077, 3077]
[33, 3077, 577, 577, 577]
[34, 577, 433, 433, 433]
[35, 433, 325, 325, 325]
[36, 325, 61, 61, 61]
[37, 61, 23, 23, 23]
[38, 23, 35, 35, 35]
[39, 35, 53, 53, 53]
[40, 53, 5, 5, 5]
[41, 5, 1, 1, 1]

sample code & (stdout) output that demonstrates the two different transducer formats compared with standard integer arithmetic calculations, for the trajectory .

tree5.rb

this generates what might be called the “collatz graph”. the graph is all integers processed by the transducer working in series, like a “sandwich”. this graph can be explored in different orders. the general idea is that a particular enumeration order might lead to more insight or some kind of regular (as opposed to quasirandom) structure that would be amenable to induction.[8] there are currently two sort orders specified, rank1 and rank2 which are switched in the rank function. the code outputs the current iteration related statistics like the size of the graph. the prior and new graph nodes codes generated are output.

tree3b.rb

this code enumerates integers in a greedy order based on the size of the ensuing transducer sequence, but without the terminating ‘1’ symbol that triggers the cascading final computation, which leads to a “cocked” transducer sequence/array (and also a natural equivalence class structure for assigning/sorting integers into). it also alternatively calculates the transducer array sequence via a recursive or fractal-like formula, and then verifies they are equal.

⭐ ⭐ ⭐

have many ideas on this problem & am more motivated to go into more detail with an engaged/interactive audience. therefore if you have any interest, reactions, or questions, please comment & it will help inspire me to continue to improve the detail of the writeup(s). note [22] is the link to lots more blog entries on the subj.

at times it feels a breakthrough is in the midst, within nearby reach, other times it all feels like a hopeless mirage not achievable in a single lifetime (there is some circumstantial evidence the problem may be undecidable, see eg [4]).

however do want to say one hopeful thing—have long strongly suspected that this problem may be resolvable with not-too-complex TCS that can not be easily/readily formulated in mathematical theory eg number theory, and the refs here would tend to support that and point in that direction.

selected refs

note: complete ref [1] is

Jeffrey O. Shallit and David W. Wilson (1991), The “3x + 1” Problem and Finite Automata, Bulletin of the EATCS (European Association for Theoretical Computer Science), No. 46, 1991, pp. 182–185.

• [1] CiteSeerX — The “3x + 1” Problem and Finite Automata / Shallit, Wilson
• [2] The 3x + 1 Problem as a String Rewriting System by Joseph Sinyor
• [3] Collatz conjecture – Wikipedia, the free encyclopedia
• [4] reference request – What is the “nearest” problem to the Collatz conjecture that has been successfully resolved? – Theoretical Computer Science
• [5] Collatz conjecture— finite state machine transducer construction, origination? – MathOverflow
• [6] AT&T FSM library
• [7] The Collatz conjecture, Littlewood-Offord theory, and powers of 2 and 3, Tao
• [8] techniques or examples of analyzing a series of graphs, cstheory
• [9] on mathematical diseases, RJ Lipton
• [10] Collatz problem/Mathworld
• [11] What is the importance of the Collatz conjecture? math.se
• [12] The 3x+1 problem: An annotated bibliography (1963–1999), Lagarias
• [13] The 3x+1 Problem: An Annotated Bibliography, II (2000-2009), Lagarias
• [14] A mathematical challenge: the 3x+1 problem, Lagarias
• [15] Collatz problem as a tag system, wikipedia
• [16] Jason Davis Collatz tree visualization
• [17] Collatz reverse tree visualization, vzn
• [18] Collatz plot thickens, vzn (introducing streaming algorithm, fractal, tree traversal algorithm angles)
• [19] A simple problems whose decidability is not known Reyzin/TCS.se
• [20] self-similarity/scale invariant/power law in integrated collatz noise vzn
• [21] Collatz Conjecture & Grammars / Automata tcs.se
• [22] vzn’s latest Collatz musings, diagrams, refs, news etc
• [23] An Analysis of the Collatz Conjecture / Motta
• [24] The Collatz conjecture and De Bruijn graphs / Laarhoven
• [25] The 3x+ 1 Problem: An Overview by Lagarias
• [26] Problems in number theory from busy beaver competition, Michel
• [27] Explorations of the Collatz conjecture / LaTourette
• [28] An update on the 3x + 1 problem / Chamberland