number theory news/ highlights: prime bias, Diffie-Hellman, Zhang-Tao, Wiles, Riemann

Leave a reply

PrimesResearchers😮 💡 ❗ 😎 😀 ❤ hi all. big news in number theory last few months and years. this is a tribute to a few years of top breakthroughs and exciting developments. the general theme is “primes” but there are a few detours.

in a breakthru/ rare event, a new statistical property of primes was discovered related to frequency of occurrence digits in base-n expansions. it was discovered by Oliver/ Soundararajan and has led to a huge amount of media attention and notice by top scientists. some of it was uncovered with dear-to-my-heart computer empirical/ experimental approaches.[e]

yet its somewhat reminiscent of another similar discovery only ~7yrs ago in 2009 by Luque/ Lacasa.[e6]

big discoveries like this sometimes make one think that maybe we havent even “scratched the surface” of theory of primes. [a2], a long-held/featured link on this site (on main sidebar) points out connections with quantum mechanics by Sautoy, an authority on the Riemann hypothesis (Dyson/ Montgomery 1972).

speaking of Riemann, and apropos/ befitting/ in observation/ reverence of todays date, it was claimed to be proven by a Nigerian recently. and it turns out not surprisingly Nigerian mathematics is not all so different than illustrious Nigerian business ventures advertised on the internet.[g]

some other blogs on this site have touched on the neat areas/ deep connections of primes, factoring, cryptography, and complexity. the Zhang-Tao breakthroughs in twin primes made massive headlines over the last few years, blogged on this awhile back and theres lots of new profiles, including New Yorker/ New York Times profiles and a video.[d][d7][d15] and in case anyone hadnt heard Zhang won the MacArthur fellowship for his work with current prize $625K.

(think its so heartening/ inspiring to see purely theoretical mathematicians get such massive admiration/ attn in our noisy/ cacaphonous/ frenetic/ vapid celebrity culture. like some others have no objections to kim kardashians (naked!) body but our culture really pushes the silly/nonsensical-limits when it refers to it as her “talent”…)

it seems we will never really exhaust all the mysteries deep in number theory and the primes seem to be the “center of gravity/ mass/ action”.

other number theory news: Wiles won the Abel prize 2016, over ~2 decades after he proved FLT.[b] ($700K but ofc whos counting?) huge congratulations but it seems a bit )( of a pity or even verging on shame he had to wait so long for this prize, and hes near retirement age. it would be great if younger researchers could win these prizes; could they do more mathematics? or even more subversively and unthinkably for many, just retire young and sip margaritas on the beach the rest of their lives?

similar news: Diffie/Hellman won the Turing award, and again it was a long ~4 decades since their work![c] (~$1M split… and again can anyone say “slow road to riches”?) their work presaged the brilliant and paradigm-shifting RSA algorithm. both are based on the complexity of the discrete log problem which is not exactly the same but highly connected with factoring. and Shors paradigm-shifting quantum algorithm also builds on this. have collected a lot of related links including excellent cryptography books. in some ways the definitive history of public key cryptography probably hasnt ever been written because, as is not recorded or even widely known by many experts, some of it is tied up with secret agencies such as GCHQ/ NSA. its also strange to ponder academics winning prizes for work that was done earlier literally in secret by “secret government agents and classified for purposes of national security”.

also speaking of subversive ideas/ crypto, for a wild time, consider the great essays by Koblitz [c16] and recent neat/ near-breakthrough paper by Rogaway[c15] “The Moral Character of Cryptographic Work” closely mirroring some of the sentiments on this blog but ofc with much more credibility.

something thats always bothered me. has anyone ever studied the actual real world performance characteristics of the AKS P-time primality testing algorithm? lack of any applied work in this area seems to attest to some of the “pie in the sky” aspects of complexity theory. more in [a].

⭐ ⭐ ⭐

another related area thats long bothered me for decades. has anyone ever looked at the automated thm proofs (ATP) for something close to the fundamental thm of arithmetic? euclids proof of the infinity of primes? its strange to me how many axioms and of such “high-level” these proofs require. cant these be reduced somehow? [f]

Euclid-Turing-vzn Prime Halting Problem Defn: given, a Turing machine F(n) that simply computes the nth prime, and fails to halt if it doesnt find one.

Problem: prove F(n) halts for all n.

Euclids proof of infinity of primes is equivalent to that F(n) halts for all n. now, how could one build a CS-like proof of this fact? eg using CS-constructions such as loop invariants etc. and if you think that the ATP proofs from the literature are it, alas, thats missing my (possibly very subtle) point, but its extremely difficult to explain why in words…

my intuition for decades has been that this all points to some kind of deep, massive, monumental undiscovered area of automated theorem proving. but its exceedingly difficult to isolate so far. speaking of isolated, apparently nobody else has the slightest whiff )( of cognitive dissonance on this but its filled me with really mounting angst for many years. maybe even thats an understatement—its nagged, haunted, nearly obsessed me.

will have to keep pondering on this zen math-CS koan, which so far, not even anyone else has noticed. what is the sound of one hand clapping?

⭐ ⭐ ⭐

all this again reminds me of one of my favorite quotes by one of my favorite mathematicians, number theorist and pure mathematican Hardy

I have never done anything ‘useful’. No discovery of mine has made, or is likely to make, directly or indirectly, for good or ill, the least difference to the amenity of the world.

Hardy must not have been talking about the primes, or maybe his sentiments were about a ~½-century premature, because they cross the divide between theory and application in startling ways. oh, that reminds me yet again, btw a fantastic new movie on Hardys collaborator Ramanujan based on the same-name book, The Man Who Knew Infinity, starring oscar-winning movie slumdog millionaire actor Patel is coming out this month, planning to blog on that one soon. dont miss it! ⭐ ❤ 😎 😀 ❗

⭐ ⭐ ⭐

these are some quick riffs on using empirical/ experimental approaches to prove the infinity of primes and my small )( contribution to the pantheon of worlds greatest results banged out on a late friday afternoon, loosely related to some of the previously employed techniques on Collatz. the underlying theme is ofc random walk manipulation.

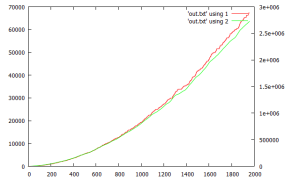
this following ruby code actually implements F(x) and has a counter for the # of total factors tested as higher integers are tested for primality. it tracks the running counter. graphed, the result is the jagged red line. long “apparently” flat areas are long sequences of consecutive “smooth” integers (having small factors quickly discovered). now, one would want to prove this line is monotonically increasing.

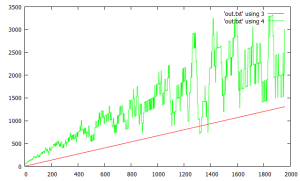
but taking differences of consecutive points shows there is not a “strong” monotonic trend. one would like to improve this monotonic trend to maybe get a “strictly monotonically increasing” line where successive points are always larger. an obvious idea is to (“running”) integrate n consecutive points, in this case 40, resulting in the much smoother green line.

then, one can take differences as found in the 2nd graph. the red line counts nonmonotonic increments of the consecutive factor counts for the “unsmoothed”/ unintegrated sequence, continually finding them. the green line is difference between consecutive points of the smoothed lines. the difference  is “always”* positive and increasing, hence the integrated count is strictly monotonically increasing. hence there are an infinity of primes. QED ❗ 😀

(* guessing the disclaimer/ fineprint left as exercise to reader.)

prime2.rb

prime2x

prime2y

(4/2) 😳 2nd thought/ 2020 hindsight, that was dashed off a bit too hastily and in my defense, was rushed/ late to a company party to drink some india 8.5% pale ale. (shew, that was close, its a good thing nobody reads this blog!) the code correctly computes primes but counting factors in the above way is not exactly correlated with primes. think a better idea, maybe the natural one struggling to break free here, is code that calculates the “prime counting function” π(x) and work with that random walk instead, proving a monotonically increasing lower bound. wow! theres maybe even some real theory on that! wonder if it can be translated into CS-language!

(4/8) another thought. cited by Wehar, Shallit et al have some interesting ideas connecting primes and DFAs, also involving digit sequences, and it shows how semi-algorithms and undecidability show up in the area even with simple questions.[h] it also has a substantial empirical/ experimental angle. it would be really great if this somewhat currently disconnected research could be connected somehow (ie also to Oliver/ Soundararajan & even Luque/ Lacasa findings)… always looking for some kind of unification…

 

a. primes
b. wiles
c. crypto/ diffie hellman
d. zhang/ tao
e. prime bias
f. auto thm proving
g. riemann
h. prime + CS

Leave a comment