happy 2nd anniversary to this blog! ⭐ ❗ 😎 😀 returning to a theme of collatz reverse tree visualization. a bunch of riffs and some other misc ideas tried out recently. nothing spectacular (in bland contrast to the last flashy-but-semimanic episode) but just posting these partly for archival/ log purposes. (brief related news, got some positive feedback on the subj on mathoverflow.)
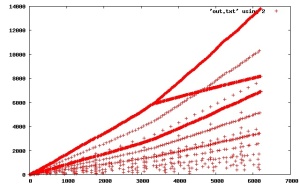
these algorithms use more complex comparison metrics, a few quadratic complexity instead of linear complexity, to decide which points to advance next. they exhibit transition-point and tipping-point like behaviors where eg there are two different regimes, one where points are scattered between horizontally increasing lines and one where they line up in “fenceposts” (vertical). (they also fix a defect noted in that earlier code where some additional spurious points (not strictly in the collatz problem) were included.)
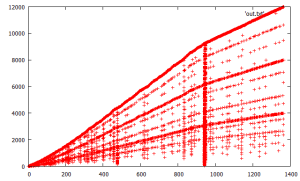
1st, find the nearest point to the prior traversed points. (arg1=5000). this took something like an hour to generate. there is a remarkable phase/regime/slope change at the fencepost for x=~940.
l2 = [2]
seen = {1 => nil}
mx = 0
j = 0
ARGV[0].to_i.times \
{
z = l2.min_by \
{
|x|
(x - seen.keys.min_by { |y| (y - x).abs }).abs
}
# p([z, l2, seen.keys])
if (z > mx) then
mx = z
j += 1
end
puts([j, z].join("\t"))
$stdout.flush
l2.delete(z)
seen[z] = nil
l = [z * 2]
l << (z - 1) / 3 if (z % 3 == 1 && ((z - 1) / 3).odd?)
l.each \
{
|x|
next if (seen.member?(x))
l2 << x
}
}
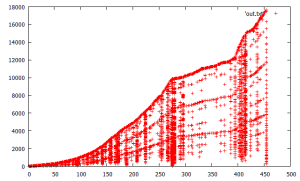
next, similar, but nonlinear weighting the x,y coordinates deltas in the next-point ranking/ comparison differently. took hours to generate.
def d(p1, x)
return 100*(p1[0] - x) ** 2 + (p1[1] - $seen[x]) ** 2
end
l2 = [[2, 0]]
$seen = {1 => 0}
mx = 0
j = 0
ARGV[0].to_i.times \
{
z = l2.min_by \
{
|x|
d(x, $seen.keys.min_by { |y| d(x, y) })
}
z0 = z[0]
if (z0 > mx) then
mx = z0
j += 1
end
puts([j, z0].join("\t"))
$stdout.flush
l2.delete(z)
$seen[z0] = mx
l = [z0 * 2]
l << (z0 - 1) / 3 if (z0 % 3 == 1 && ((z0 - 1) / 3).odd?)
l.each \
{
|x|
next if ($seen.member?(x))
l2 << [x, mx]
}
}
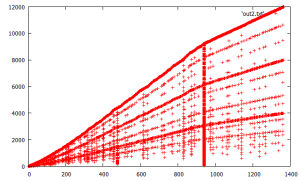
next, a linear time comparison algorithm instead of quadratic, just try to find nearest points to current previously seen point average. this is surprisingly, strikingly nearly identical to plot #1. a strange attractor?
l2 = [2]
seen = {1 => nil}
mx = 0
j = 0
ARGV[0].to_i.times \
{
a = 0
seen.keys.each { |x| a += x }
a = a.to_f / seen.size
z = l2.min_by \
{
|x|
(x - a).abs
}
# p([z, l2, seen.keys])
if (z > mx) then
mx = z
j += 1
end
puts([j, z].join("\t"))
$stdout.flush
l2.delete(z)
seen[z] = nil
l = [z * 2]
l << (z - 1) / 3 if (z % 3 == 1 && ((z - 1) / 3).odd?)
l.each \
{
|x|
next if (seen.member?(x))
l2 << x
}
}
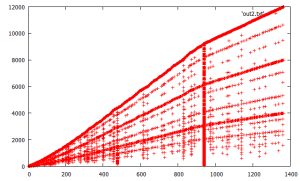
next, this code attempts to balance out by selecting new points in the “midpoints” of the prior point cloud, where there are the largest gaps. again a quadratic time algorithm.
l2 = [2]
seen = {1 => nil}
mx = 0
j = 0
ARGV[0].to_i.times \
{
l = seen.keys.sort
m = 0
z = nil
l2.each \
{
|x|
i = 0
i += 1 while (i < l.size && x > l[i])
next if (i == l.size)
a = i > 0 ? l[i - 1] : 0
b = l[i]
r = (x - a) * (b - x)
z, m = x, r if (r > m)
}
if (z.nil?) then
z = l2.min
j += 1
end
puts([j, z].join("\t"))
$stdout.flush
l2.delete(z)
seen[z] = nil
l = [z * 2]
l << (z - 1) / 3 if (z % 3 == 1 && ((z - 1) / 3).odd?)
l.each \
{
|x|
next if (seen.member?(x))
l2 << x
}
}
its remarkable that very different adaptive algorithms lead to the overall same output structure, suggesting some kind of resilience or strange attractor. there are small differences in the output ordering of points but the algorithms converge to similar overall structures. and getting nearly identical results with the linear vs quadratic measurement is also surprising.
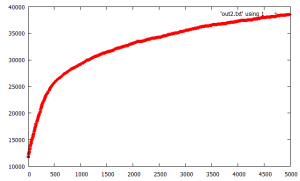
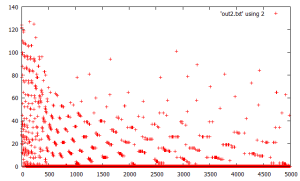
next, this seems like a notable finding. this is similar to an earlier idea of using a fixed-sized “relatively small” running buffer (200 points) and extracting min points from the buffer. the semi surprising finding is that the total buffer integration is orderly monotonically increasing. 2nd graph shows deltas between adjacent curve points.
def f(n)
c = 0
while (n != 1)
n = n.even? ? n / 2 : n * 3 + 1
c += 1
end
return c
end
l = []
n = 3
t = 0
w = 200
t2 = nil
(w + 5000).times \
{
x = f(n)
l << x
t += x
if (l.size > w) then
i = (0...l.size).min_by { |j| l[j] }
t -= l[i]
l.delete_at(i)
puts([t, t - t2].join("\t")) if (!t2.nil?)
t2 = t
end
n += 2
}
its also naturally worth looking at the “age” of points removed from the buffer.
def f(n)
c = 0
while (n != 1)
n = n.even? ? n / 2 : n * 3 + 1
c += 1
end
return c
end
l = []
n = 3
t = 0
w = 200
t2 = nil
a = 0
m = 20000
(w + m).times \
{
x = f(n)
l << [x, n]
t += x
if (l.size > w) then
i = (0...l.size).min_by { |j| l[j] }
p = l[i][1]
t -= l[i][0]
l.delete_at(i)
puts([t, n - p, t - t2].join("\t")) if (!t2.nil? && a > m - 10000)
t2 = t
end
n += 2
a += 1
}
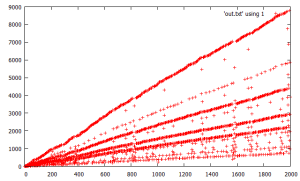
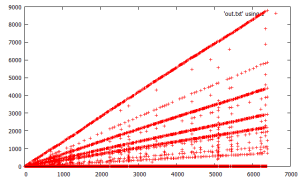
(10/25) this following simple code uses a 1000 point buffer and iterates forward through the smallest element, and replaces it with the next sequential unexplored/ unterminated integer if its trajectory reaches 1. the 1st graph is the new points added to the buffer and the 2nd graph is the “resolved” points, where gaps in the 1st correspond to no new point(s) added during that iteration and the buffer processed (smallest element advanced). the algorithm outputs resolved points in batches as new unverified trajectories “hit/touch” the verified trajectories; this is roughly the same as trajectory merge logic described earlier. the 2nd graph is notable in that “higher” points are very regular in their spacing/ alignment and the plot gets more random/ scattered as moving to “lower” points. it also shows a notable/ major regime change around x=~3200 seen in in the top line slope change and “fork/ bifurcation” and also coinciding/ corresponding with a prior gap in the first graph.
#!/usr/bin/ruby1.8
l = []
seen = {}
done = {1 => nil}
n = -1
1000.times \
{
n += 4
seen[n] = l.size
l << [n]
}
5000.times \
{
i = -1
l2 = l.map { |l1| [l1[-1], i += 1] }
n2, i = l2.min
puts([0, n2].join("\t"))
n2 = (n2 % 2 == 0) ? n2 / 2 : n2 * 3 + 1
if (done.member?(n2)) then
l[i].each { |x| done[x] = nil; p(x) }
l[i] = [n += 4]
end
if (!(j = seen[n2]).nil?)
x = l[j][-1]
l[j] |= l[i]
l[j] << x
l[i] = [n += 4]
seen[n] = i
else
l[i] << n2
seen[n2] = i
end
}
(10/28) returning to another idea touched on earlier. those experiments showed an apparently level (constant bounded?) vertex count of blockwise-piece graphs even for very high trajectories. based on a remarkable property associated with transducer constructions of TMs, if any TM can be constructed that resolves all values of the problem (or any other problem) in a constant number of iterations, that is provable within the transducer framework. the details are somewhat involved but not actually very complex.
however, presumably these graphs are misleading. from an earlier experiment (end of the same post), apparently arbitrarily long sequences/ trajectories exist, although not so sure how to prove this. they might be or seem to be hidden “outside” the monte carlo samples like (very rare?) needles buried in the haystack. anyway with that caveat, here is another experiment surveying the haystack up to large initial trajectories and showing the standard deviation error bars. the “apparently constant property” is visible, but this maybe also shows/ demonstrates the limitations of visualizations, and the limitations of aggregate statistics (averages) esp with non-gaussian & fractal distributions (popularized by Nassem Taleb as the so-called “black swan” phenomenon). this randomly samples the space up to with 5000 samples at each interval, each 1000 trajectory blockwise piece graphs and shows no discernable slope.
def f(n)
n2 = n
while (n2 >= n)
n2 = n2.even? ? n2 / 2 : n2 * 3 + 1
break if ($seen.member?(n2))
$seen[n2] = nil
end
end
def sample(n, c, w)
t = t2 = 0
c.times \
{
m = 2 ** n + rand(2 ** n) | 1
$seen = {}
w.times \
{
f(m)
m += 2
}
x = $seen.size
t += x
t2 += x**2
}
a = t.to_f / c
return a, Math.sqrt(t2.to_f / c - a ** 2)
end
n = 20
50.times \
{
a, sd = sample(n, 5000, 1000)
puts([n, a, sd].join("\t"))
$stdout.flush
n += 20
}
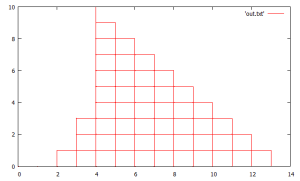
(10/31) revisiting the “valid suffix/prefix enumeration” code. (recall) this code looks at binary suffixes for initial seeds that dont “fall below” and recursively generates them. an interesting factoid is that this tree always has at least one (min) or two branches (max) at each node, never zero. it lists the source prefix and then the 1 or 2 new branching prefixes as indented. not sure how to prove this at the moment. it seems to have something to do with prefixes being in the form . this also does a histogram of ‘1’s found in the binary prefixes, they seem to be somewhat smoothly or normally distributed. ARG[0] = 10
def check(n, b)
a = n
b0 = b
while (a >= n)
if (b.odd?) then
a *= 3
b = b * 3 + 1
end
if (b.even?) then
if (!a.even?) then
return [b0]
end
a /= 2
b /= 2
end
end
return []
end
def scan(p)
n = 2**p
l = []
(1...n).each \
{
|i|
l += check(n, i)
a = n
b = i
}
return l
end
def wrap(p, x, n)
l = check(2 ** p, x)
return [] if (l.empty?)
puts("\t"+sprintf("%0#{p}d", l[0].to_s(2)).reverse)
return l
end
def recur(n)
l = [1]
(2..n).each \
{
|p|
l2 = []
l.each \
{
|x|
puts(sprintf("%0#{p - 1}d", x.to_s(2)).reverse)
l2 += wrap(p, x, n)
l2 += wrap(p, x + (2 ** (p - 1)), n)
}
puts("---")
l = l2
}
return l
end
n = ARGV[0].to_i
l2 = recur(n)
h = {}
l2.each \
{
|x|
c = x.to_s(2).split('').select { |y| y == '1' }.size
h[c] = 0 if (h[c].nil?)
h[c] += 1
}
p(h)
1
11
---
11
110
111
---
110
1101
111
1110
1111
---
1101
11011
1110
11100
1111
11110
11111
---
11011
110110
110111
11100
111000
111001
11110
111100
111101
11111
111110
111111
---
110110
1101100
1101101
110111
1101111
111000
1110001
111001
1110010
1110011
111100
1111001
111101
1111010
1111011
111110
1111100
1111101
111111
1111110
1111111
---
1101100
11011000
11011001
1101101
11011010
1101111
11011111
1110001
11100010
1110010
11100101
1110011
11100110
11100111
1111001
11110011
1111010
11110100
1111011
11110110
11110111
1111100
11111000
11111001
1111101
11111011
1111110
11111100
11111101
1111111
11111110
11111111
---
11011000
110110000
110110001
11011001
110110010
110110011
11011010
110110100
110110101
11011111
110111110
110111111
11100010
111000100
111000101
11100101
111001010
111001011
11100110
111001100
111001101
11100111
111001110
111001111
11110011
111100110
111100111
11110100
111101000
111101001
11110110
111101100
111101101
11110111
111101110
111101111
11111000
111110000
111110001
11111001
111110010
111110011
11111011
111110110
111110111
11111100
111111000
111111001
11111101
111111010
111111011
11111110
111111100
111111101
11111111
111111110
111111111
---
110110000
1101100000
1101100001
110110001
1101100010
1101100011
110110010
1101100100
1101100101
110110011
1101100110
110110100
1101101000
1101101001
110110101
1101101011
110111110
1101111100
1101111101
110111111
1101111111
111000100
1110001000
111000101
1110001010
1110001011
111001010
1110010100
1110010101
111001011
1110010111
111001100
1110011000
1110011001
111001101
1110011010
1110011011
111001110
1110011100
1110011101
111001111
1110011110
111100110
1111001100
1111001101
111100111
1111001110
111101000
1111010000
1111010001
111101001
1111010010
111101100
1111011000
1111011001
111101101
1111011011
111101110
1111011100
1111011101
111101111
1111011110
1111011111
111110000
1111100000
1111100001
111110001
1111100011
111110010
1111100100
1111100101
111110011
1111100110
1111100111
111110110
1111101100
111110111
1111101110
1111101111
111111000
1111110000
111111001
1111110010
1111110011
111111010
1111110100
1111110101
111111011
1111110110
1111110111
111111100
1111111000
1111111001
111111101
1111111010
1111111011
111111110
1111111100
1111111101
111111111
1111111110
1111111111
---
{4=>2, 5=>9, 6=>16, 7=>17, 8=>12, 9=>7, 10=>1}
this is some funky code that visualizes the prefixes using a simple random walk-like approach & shows how it is constrained/ confined in a remarkable stairstep pattern, and also helps to show/ understand how the 1’s are ordered/ distributed inside the binary expansion. (has a sort of zen-like simplicity eh?) 😎 the 2nd graph uncomments the offsetting feature/ line. ARGV[0] = 14
def check(n, b)
a = n
b0 = b
while (a >= n)
if (b.odd?) then
a *= 3
b = b * 3 + 1
end
if (b.even?) then
if (!a.even?) then
return [b0]
end
a /= 2
b /= 2
end
end
return []
end
def scan(p)
n = 2**p
l = []
(1...n).each \
{
|i|
l += check(n, i)
a = n
b = i
}
return l
end
def wrap(p, x, n)
l = check(2 ** p, x)
return [] if (l.empty?)
# puts("\t"+sprintf("%0#{p}d", l[0].to_s(2)).reverse)
return l
end
def recur(n)
l = [1]
(2..n).each \
{
|p|
l2 = []
l.each \
{
|x|
# puts(sprintf("%0#{p - 1}d", x.to_s(2)).reverse)
l2 += wrap(p, x, n)
l2 += wrap(p, x + (2 ** (p - 1)), n)
}
# puts
l = l2
}
return l
end
n = ARGV[0].to_i
l2 = recur(n)
l2.each_with_index \
{
|x, i|
s = sprintf("%0#{n}d", x.to_s(2)).reverse
x = y = 0 #i * 0.0007
s.split('').each \
{
|b|
puts([x, y].join("\t"))
b == '1' ? x += 1 : y += 1
puts([x, y].join("\t"))
puts
}
}
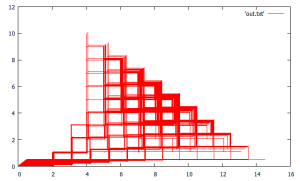
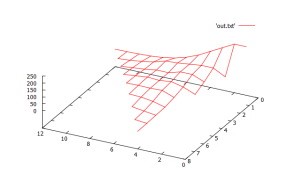
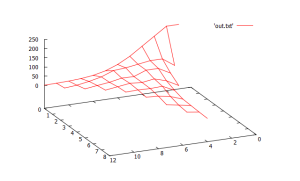
another natural/ nice way of visualizing these results is a 3d “surface plot histogram”, 2 perspective angles below. here point height is the histogram count and (x, y) is the intermediate location/ visits of the walks. using this method, the starting location (0,0) has the highest count and counts decrease from there. this also highlights the smoothness of the distribution. another obvious idea is to just graph the counts of ending locations.
def check(n, b)
a = n
b0 = b
while (a >= n)
if (b.odd?) then
a *= 3
b = b * 3 + 1
end
if (b.even?) then
if (!a.even?) then
return [b0]
end
a /= 2
b /= 2
end
end
return []
end
def scan(p)
n = 2**p
l = []
(1...n).each \
{
|i|
l += check(n, i)
a = n
b = i
}
return l
end
def wrap(p, x, n)
l = check(2 ** p, x)
return [] if (l.empty?)
# puts("\t"+sprintf("%0#{p}d", l[0].to_s(2)).reverse)
return l
end
def recur(n)
l = [1]
(2..n).each \
{
|p|
l2 = []
l.each \
{
|x|
# puts(sprintf("%0#{p - 1}d", x.to_s(2)).reverse)
l2 += wrap(p, x, n)
l2 += wrap(p, x + (2 ** (p - 1)), n)
}
# puts
l = l2
}
return l
end
n = ARGV[0].to_i
l2 = recur(n)
h = {}
l2.each_with_index \
{
|x, i|
s = sprintf("%0#{n}d", x.to_s(2)).reverse
x = y = 0
s.split('').each \
{
|b|
b == '1' ? x += 1 : y += 1
z = [x, y]
h[z] = 0 if (h[z].nil?)
h[z] += 1
}
}
def fmt(p, h)
return (p + [h[p]]).join("\t")
end
h.sort.each \
{
|p0, z|
p1 = [p0[0] + 1, p0[1]]
p2 = [p0[0], p0[1] + 1]
[p1, p2].each \
{
|p|
printf("%s\n%s\n\n\n", fmt(p0, h), fmt(p, h)) if (h.member?(p))
}
}
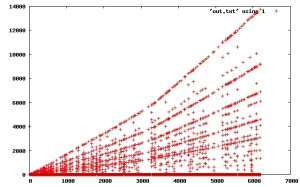
(11/4) heres another idea where trajectories are resolved in parallel, working from min elements in the trajectory frontiers, but not by ending at 1 and instead resolved at the “fall below” point. it uses a “reverse-directed” graph/tree of the trajectories to mark resolved points and again a typical “seen” cache to recognize previously visited/ processed points. the “mark” subroutine is a breadth-1st reverse/ backward traversal of an “in flight” trajectory converted to “resolved”. the 2nd plot is with the commented line uncommented and puts in “zero” points for loop iterations where new trajectories are started. it leads to a more ordered/ linear plot.
def mark(n)
l = [n]
while (!l.empty?)
n = l.shift
next if ($seen.member?(n))
$c += 1
p(n)
$seen[n] = nil
l.push(*$back[n].keys) if ($back.member?(n))
end
end
at = {1 => 1}
m = 3
$back = {}
$seen = {}
$c = 0
loop \
{
l = at.to_a.min
if (l.nil? || m < l[0]) then
a = n = m
m += 2
# puts([0, n].join("\t"))
else
n, a = l
at.delete(n)
end
n2 = n.even? ? n / 2 : n * 3 + 1
$back[n2] = {} if ($back[n2].nil?)
$back[n2][n] = nil
if (n2 > a)
at[n2] = at[n2].nil? ? a : [a, at[n2]].min
else
mark(n2)
end
break if ($c == 2000)
}
(11/7) this is a natural question about how a depth first versus a breadth first search of prefix enumeration leads to larger trajectories. the idea is to mix some breadth exploration with the depth-first exploration. the output in (a, b, c, d) format shows that about 10 breadth iterations per depth iteration leads to about 30% longer trajectories (column a) at the cost of a larger frontier set, but the “gain” mostly flattens/ plateaus out after that. b is the size of the starting seed in bits, c is the size of the frontier set, and d is the iteration.
def count(n)
c = 0
while (n != 1)
n = n.even? ? n / 2 : n * 3 + 1
c += 1
end
return c
end
def check(p, b)
n = 2 ** p
a = n
b0 = b
c = 0
while (a >= n)
if (b.odd?) then
a *= 3
b = b * 3 + 1
else
return [[b0, c + count(b), p + 1]] if (!a.even?)
a /= 2
b /= 2
end
c += 1
end
return []
end
def recur3(m, j)
l = [[1, 0, 2]]
t = 0
loop \
{
l.sort_by! { |x, c, p| -c }
t += 1
break if (t >= m)
j.times \
{
x, c, p = l.shift
l += check(p, x)
l += check(p, x + (2 ** (p - 1)))
}
}
p(l[0][1..2] + [l.size, j])
return l
end
m = 150
(1..20).each { |j| l2 = recur3(m, j) }
[1401, 133, 128, 1] [1443, 146, 257, 2] [1935, 153, 417, 3] [1691, 146, 517, 4] [1879, 155, 720, 5] [1860, 155, 852, 6] [2049, 154, 992, 7] [1863, 156, 1115, 8] [1821, 155, 1297, 9] [1979, 155, 1424, 10] [1814, 156, 1542, 11] [1902, 156, 1708, 12] [2100, 157, 1892, 13] [2100, 157, 2034, 14] [2100, 157, 2183, 15] [1998, 157, 2330, 16] [2100, 157, 2460, 17] [2142, 157, 2638, 18] [1774, 157, 2710, 19] [2009, 158, 2911, 20]
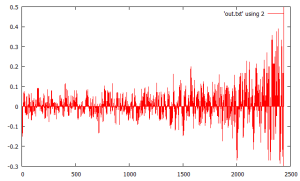
this code looks at the density of 1s in the binary expansion of trajectory points for a long 200 “depth” trajectory (length 2439 iterations). it reminds me of research onto the “knife edge” point of satisfiability. it shows that long trajectories apparently have a fractal-like self similar structure where density of 1s in iterates tends to hover around 50%, and the divergence/ deviation tends to widen at the end.
there is an interesting way to view/ interpret this in terms of complexity “hardness” with more parallels to the SAT knife edge. the time to resolve the trajectory is like the complexity of the algorithm. an instance is recursively resolved. if the next instance is self-similar to the previous instance (iterate), hardness is maximized.
def count(n)
c = 0
while (n != 1)
n = n.even? ? n / 2 : n * 3 + 1
c += 1
end
return c
end
def check(p, b)
n = 2 ** p
a = n
b0 = b
c = 0
while (a >= n)
if (b.odd?) then
a *= 3
b = b * 3 + 1
else
return [[b0, c + count(b), p + 1]] if (!a.even?)
a /= 2
b /= 2
end
c += 1
end
return []
end
def recur3(m, j)
l = [[1, 0, 2]]
t = 0
loop \
{
l.sort_by! { |x, c, p| -c }
t += 1
break if (t >= m)
j.times \
{
x, c, p = l.shift
l += check(p, x)
l += check(p, x + (2 ** (p - 1)))
}
}
return l[0][0]
end
def density(n)
while (n != 1)
n = n.even? ? n / 2 : n * 3 + 1
c = 0
s = n.to_s(2)
s.split('').each { |x| c += x.to_i }
puts([Math.log(n), c.to_f / s.length - 0.5].join("\t"))
end
end
n = recur3(200, 10)
density(n)
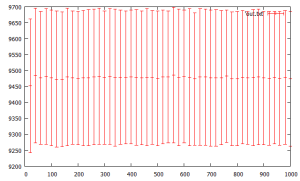
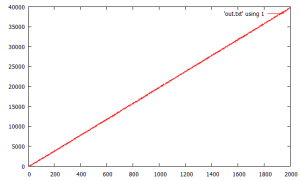
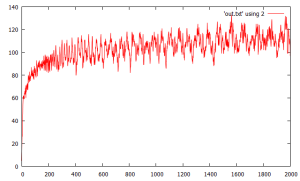
(11/19) this is some straightforward code that achieves a very nice balance of outputting resolved trajectory seeds in an almost linear fashion with a slowly increasing buffer size. it simply advances a large buffer of current trajectories each in parallel and always adds the current iterate to the (end of the) buffer. it has no logic to deal with previously seen iterates. there is a little extra logic to look at the last trend versus the output summarized overall trend. 1st graph is the resolved seeds and second is the buffer size.
def f(x)
x = x.even? ? x / 2 : x * 3 + 1
end
l = []
l3 = []
l4 = []
c = 2000
m = 20000
d = m.to_f / c
n = 3
m.times \
{
|j|
l << [n]
n += 2
i = 0
while (i < l.size)
l[i] << f(l[i][-1])
if (l[i][-1] == 1) then
l2 = l.delete_at(i)
l3 << [l2[0], l.size]
l4 << l3[-1] if (l4.size < j / d)
l3.shift if (l3.size > c)
next
end
i += 1
end
}
#p(l4.size)
l4.each { |x| puts(x.join("\t")) }
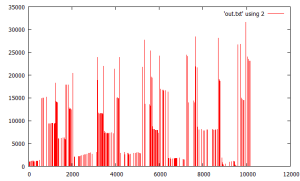
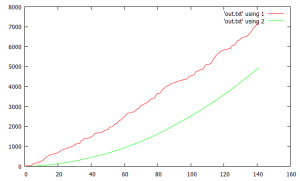
another quick idea reminiscent of an earlier one. this code sequentially accumulates trajectory lengths in a way that enforces a “minimally” monotonically increasing trend (red). it tracks which seeds cross new maximum boundaries. this results in a very orderly graph of the 2nd statistic (green).
def f(n)
c = 0
while (n != 1)
n = n.even? ? n / 2 : n * 3 + 1
c += 1
end
return c
end
m = 1
m2 = 0
n = 3
5000.times \
{
|j|
m2 += f(n)
if (m2 > m) then
m = m2
m2 = 0
puts([m, j].join("\t"))
end
n += 2
}
Pingback: Collatz, striking visualization of binary density for 3x + 1 operation! | Turing Machine
Pingback: ***startling*** collatz plateau! | Turing Machine